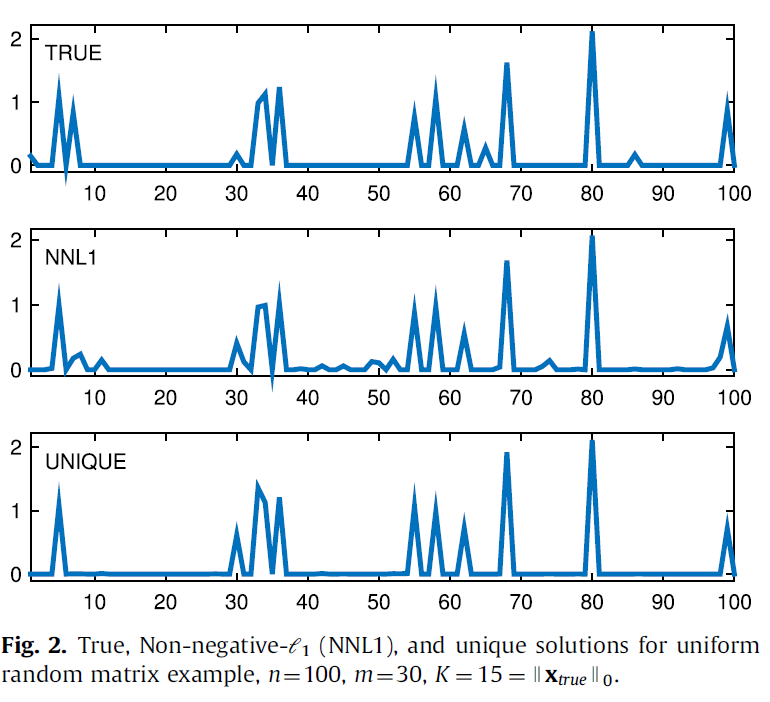
In this paper we take a novel approach to the regularization of underdetermined linear systems. Typically, a prior distribution is imposed on the unknown to hopefully force a sparse solution, which often relies on uniqueness of the regularized solution (something which is typically beyond our control) to work as desired. But here we take a direct approach, by imposing the requirement that the system takes on a unique solution. Then we seek a minimal residual for which this uniqueness requirement holds.
When applied to systems with non-negativity constraints or forms of regularization for which sufficient sparsity is a requirement for uniqueness, this approach necessarily gives a sparse result. The approach is based on defining a metric of distance to uniqueness for the system, and optimizing an adjustment that drives this distance to zero. We demonstrate the performance of the approach with numerical experiments.
K. Dillon and Y.-P. Wang, “Imposing uniqueness to achieve sparsity,” Signal Processing, vol. 123, pp. 1–8, Jun. 2016. (pdf)