BDS 761: Data Science and Machine Learning I


drawing

Topic 4: Python Math Basics

This topic:¶

  1. Basic math in python
  2. Vectors and Matrices in Python

Readings:

  • data science tutor GPT: https://chatgpt.com/g/g-SSBhmwHol-introductory-data-science-tutor
  • I2ALA Chapter 1
  • Chapter zero of "Coding the Matrix"

0. Motivation¶

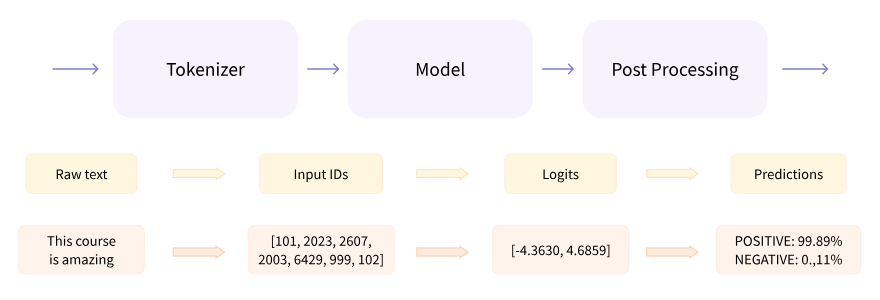
Hugging Face Pipelines: Base class implementing NLP operations. Pipeline workflow is defined as a sequence of the following operations:

  • A tokenizer in charge of mapping raw textual input to token --> string (or other data format) processing
  • A model to make predictions from the inputs --> linear algebra
  • Some (optional) post processing for enhancing model’s output --> misc
drawing

https://huggingface.co/docs/transformers/en/main_classes/pipelines

Behind the pipeline¶

drawing

https://huggingface.co/learn/nlp-course/chapter2/2

Inside the Model¶

drawing

Inside the GPU¶

General Matrix Multiplication (GEMM) ~ $C = \alpha AB + \beta C$

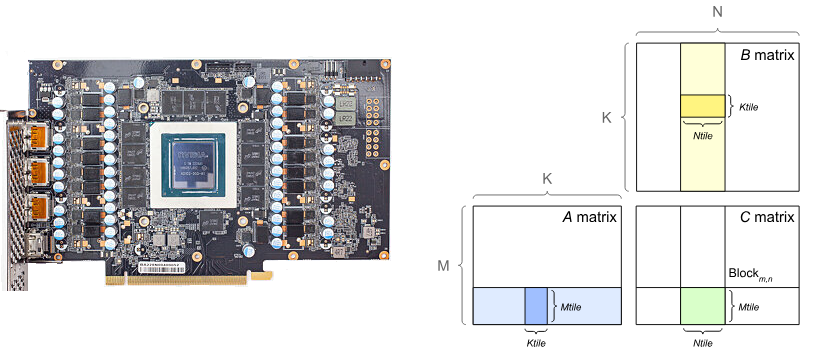
drawing

https://docs.nvidia.com/deeplearning/performance/dl-performance-matrix-multiplication/index.html

Basic Abstract Mathematics¶

  • Sets
  • Functions
  • Procedure
  • Inverse function

Sets¶

  • Elements
  • Subsets
  • Cardinality
  • Reals
  • Cartesian products of sets

Function¶

  • Rule that assigns input to output
  • Mapping between sets
  • Image
  • Pre-image
  • Domain
  • Co-domain
  • Composition
  • Probablity as a function

Procedure¶

  • Description of a computation
  • Also called "function"
  • Versus "computational problem"

Inverse function¶

  • Forward versus Backward Problem
  • One-to-one
  • Onto
  • Of composition

Fields¶

A set with "+" and "x" operations (that work properly).

  • Reals $\bf R$
  • Complex numbers $\bf C$
  • GF(2)

I. Python Math¶

  • Data structures
  • Programming

Numerical precision¶

  • Bytes/words, ints, floats, doubles... how big are they?

  • IEEE 745 standard numerical arithmetic

  • nan, inf, eps

  • "Hard zeros"

Basic Python Data Structures ("collections")¶

  • Sets
  • Lists
  • Tuples
  • Dictionaries

Sets {item1, item2, item3}¶

  • Order is not necessarily maintained
  • Each item occurs at most once
  • Mutable

Create a set with a repeated value in and print it

In [4]:
S={1,2,2,3}
print(S)

{1, 2, 3}

Compute the cardinality of your set

In [5]:
print(len(S))

3
In [7]:
T = S.copy()

T.add(6)
print(T)
print(S)

{1, 2, 3, 6}
{1, 2, 3}

Sets ...continued¶

Other handy functions

  • sum()
  • logical test for membership
  • add(), remove(), update()
  • copy() -- NOTE: Python "=" binds LHS to RHS by reference, it is not a copy.

Q: Is a set a good data structure to make vectors and do linear algebra?

Lists [item1, item2, item3]¶

  • Sequence of values - order & repeats ok
  • Mutable
  • Concatenate lists with "+"
  • Index with mylist[index] - note zero based

Convert your set to a list, print list, its length, it's first and last elements

In [31]:
L = list(S)
print(L)
print("length =",len(L))
print(L[0],L[2])

[1, 2, 3]
length = 3
1 3
In [27]:
[1,2,3,4,5][3]
Out[27]:
4

Slices - mylist[start:end:step]¶

Matlabesque way to select sub-sequences from list

  • If first index is zero, can omit - mylist[:end:step]
  • If last index is length-1, can omit - mylist[::step]
  • If step is 1, can omit mylist[start:end]

Make slices for even and odd indexed members of your list.

Q: Is this a good data structure to make vectors and do linear algebra?

Tuples (1,2,3)¶

  • Immutable version of list basically
In [25]:
(1,2,3)[1] # note can access directly
Out[25]:
2
  • Handy for packing info
  • sometimes omit the parenthesis
In [23]:
1,2
Out[23]:
(1, 2)

The constructors¶

  • convert other collections (and iterators) into collections
In [32]:
L = list(S)
S = set(L)
T = tuple(S)

Dictionaries {key1:value1,key2:value2}¶

  • key:value ~ word:definition
  • access like a generalized list
In [38]:
mydict = {0:100,1:200,3:300}
mydict[0]
Out[38]:
100
In [29]:
mydict = {'X':'hello','Y':'goodbye'}
mydict['X']
Out[29]:
'hello'
In [32]:
mydict.items()
Out[32]:
dict_items([('X', 'hello'), ('Y', 'goodbye')])

Dictionaries ...continued¶

  • keys()
  • values()
  • items()

How would you use a dictionary to make a vector?

Basic Python Programming¶

  • Comprehensions
  • Loops
  • Whitespace
  • Conditional statements
  • Functions

Comprehensions¶

  • Use iterators for generating sets/lists/tuples
  • Similar to mathematical set notation
  • popular in "Coding the Matrix"
In [30]:
L=list(i for i in {1,2,3})
print(L)

[1, 2, 3]
In [55]:
dict((mydict[key],key) for key in mydict)
Out[55]:
{'hello': 'X', 'goodbye': 'Y'}

Iterate over list and produce list squared

In [56]:
L=[1,1,2,3,4,4,5]
In [59]:
LL = list([x,y] for x in [1,2,3] for y in [1,2,3])
LL
Out[59]:
[[1, 1], [1, 2], [1, 3], [2, 1], [2, 2], [2, 3], [3, 1], [3, 2], [3, 3]]

Loops¶

In [35]:
for x in {1,2,3}:    
    print(x)
    print(x*x)

1
1
2
4
3
9

Whitespace¶

  • used for grouping code
  • same indent = same group
  • nested code = increased indent
  • must be used properly
In [69]:
for x in {1,2,3}: 
    print(x)
    for y in {1,2,3}: 
        print('...',x,y)

1
... 1 1
... 1 2
... 1 3
2
... 2 1
... 2 2
... 2 3
3
... 3 1
... 3 2
... 3 3
In [45]:
x=0
while x<5:
    print(x)
    x=x+1

0
1
2
3
4

Range Function¶

In [75]:
list(range(10,0,-1))
Out[75]:
[10, 9, 8, 7, 6, 5, 4, 3, 2, 1]
In [74]:
for x in range(0,10):
    print(x)

0
1
2
3
4
5
6
7
8
9

Conditional Statements¶

In [47]:
if not (2+2 == 4):     
    print('tree')
else:
    print('hi')

hi

Defining functions¶

In [107]:
def myfunc(x):
    print(x)
    return x**2
    
myfunc(4)

4
Out[107]:
16

III. Vectors & Matrices¶

Vector - Multiple numbers "drawn from a field"¶

A $k$-dimensional vector $y$ is an ordered collection of $k$ numbers $y_1 , y_2 , . . . , y_k$ written as $\textbf{y} = (y_1,y_2,...,y_k)$.

The numbers $y_j$, for $j = 1,2,...,k$, are called the $\textbf{components}$ of the vector $y$.

Note boldface for vectors and italic for scalars, a popular convention.

It can be written either as rows (math, engineering) or columns (CS, statistics), and we won't worry about this.

$$\textbf{y} = \begin{bmatrix} y_1 \\y_2 \\ \vdots \\ y_k \end{bmatrix} = [y_1,y_2,...,y_k]^{T} $$

(Swapping rows and columns = transposing. 1st column = top. 1st row = left.)

Vector Examples¶

  1. string?

  2. Coordinates

  3. Direction

  4. GPS entry

  5. Collection of clinical study data for single individual ("sample" in machine learning).

  6. An image

  7. A music or voice signal

  8. A block of binary data

Consider the numbers we want to use for each.

Data Science Examples of vectors¶

A list of data for different "dimensions", for one person, product, etc.

drawing

-Yaser Abu-Mostafa, Learning From Data

KEY FACT: The position in the vector is special, e.g. $x$ versus $y$, age versus gender.¶

Drawn from a Field?¶

Recall a field is a set. So a vector has each member from the set.

  • Vector of real numbers $\mathbf v \in \mathbf R^n$

  • Vector of binary numbers $\mathbf b \in GF(2)^n$

What is the notation for our previous examples?

Data Structure Options¶

  • Python Sets
  • Python Lists
  • Python Tuples
  • Python Dictionaries

Consider how you would use each of these to make a vector of coordinates.

Recall the other kinds of info we make into vectors. Does the data structure work for all of them?

Vector Addition $\mathbf a + \mathbf b$¶

Addition of two k-dimensional vectors $\textbf{x} = (x_1, x_2, ... , x_k)$ and $\textbf{y} = (y_1,y_2,...,y_k)$ is defined as a new vector $\textbf{z} = (z_1,z_2,...,z_k)$, denoted $\textbf{z} = \textbf{x}+\textbf{y}$,with components given by $z_j = x_j+y_j$.

Vector Addition $\mathbf a + \mathbf b$¶

Addition of corresponding entries.

Geometrical perspective.

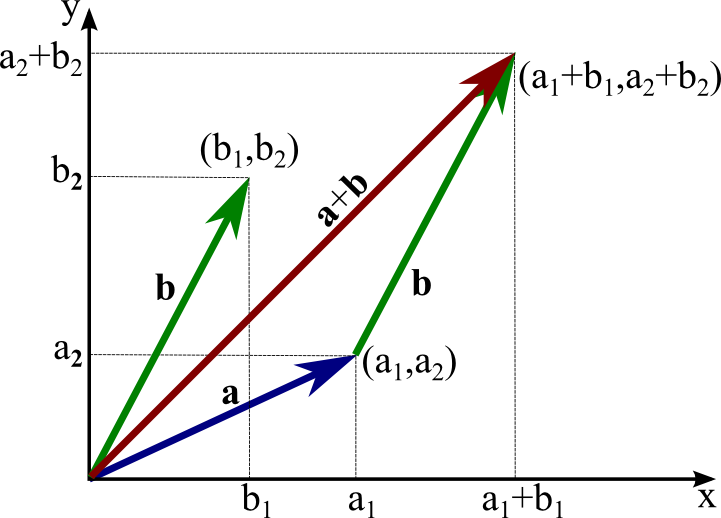
drawing

Consider in terms of applications.

Scalar-Vector multiplication $\alpha \mathbf y$¶

Scalar multiplication of a vector $\textbf{y} = (y_1, y_2, . . . , y_k)$ and a scalar α is defined to be a new vector $\textbf{z} = (z_1,z_2,...,z_k)$, written $\textbf{z} = \alpha\ \textbf{y}$ or $\textbf{z} = \textbf{y} \alpha$, whose components are given by $z_j = \alpha y_j$.

Code these operations in Python¶

Consider vectors describing distance travelled in 2D.

Make two functions:

  • multiply a vector of data by a scalar (i.e. "scale it")

  • add two vectors.

  • Make it work for any number of dimensions

The Dot Product $\mathbf x \cdot \mathbf y$¶

If we have two vectors: ${\bf{x}} = (x_1, x_2, ... , x_k)$ and ${\bf{y}} = (y_1,y_2,...,y_k)$

The dot product is written: ${\bf{x}} \cdot {\bf{y}} = x_{1}y_{1}+x_{2}y_{2}+\cdots+x_{k}y_{k}$

If $\mathbf{x} \cdot \mathbf{y} = 0$ then $x$ and $y$ are orthogonal

What is $\mathbf{x} \cdot \mathbf{x}$?

Applications¶

  • Measuring similarity

  • Customer profile comparison

drawing

Applications¶

You may have heard of this little guy:

drawing

Code the dot product in Python¶

  • Choose appropriate data structures for your vectors

  • Make it work for any number of dimensions

Properties of Dot Product¶

  • Commutative
  • Homogeneous
  • Distributes over vector addition

Test them with your code and example vectors

Homogeneity: $(\alpha \mathbf x) \cdot \mathbf y = \alpha (\mathbf x \cdot \mathbf y)$¶

Consider what this means for using the dot product to measure similarity.

Use your functions to implement this both ways.

Classes in Python¶

Clunky but handy to encapsulate related code

Note odd way that constructor is defined

Also need to pass "self" argument to every function

In [28]:
class Complex:
    def __init__(self, realpart, imagpart):
        self.r = realpart
        self.i = imagpart
x = Complex(3.0, -4.5)
x.r, x.i
Out[28]:
(3.0, -4.5)

Python Lab¶

Make a class for "dense" vectors that contains all your functions thus far.

Add methods for handling sparse vectors:

  1. Vector addition
  2. Scalar-vector multiplication
  3. Dot product

Compare speed to large dense vectors for different levels of density.

Advanced: compare to sparse vectors in numpy.

Matrices¶

A matrix $\mathbf A$ is a rectangular array of numbers, of size $m \times n$ as follows:

$\mathbf A = \begin{bmatrix} A_{1,1} & A_{1,2} & A_{1,3} & \dots & A_{1,n} \\ A_{2,1} & A_{2,2} & A_{2,3} & \dots & A_{2,n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ A_{m,1} & A_{m,2} & A_{m,3} & \dots & A_{m,n} \end{bmatrix}$

Where the numbers $A_{ij}$ are called the elements of the matrix. We describe matrices as wide if $n > m$ and tall if $n < m$. They are square iff $n = m$.

NOTE: naming convention for scalars vs. vectors vs. matrices.

Scalar Multiplication¶

Scalar multiplication of a matrix $\textit{A}$ and a scalar α is defined to be a new matrix $\textit{B}$, written $\textit{B} = \alpha\ \textit{A}$ or $\textit{B} = \textit{A} \alpha$, whose components are given by $b_{ij} = \alpha a_{ij}$.

Matrix Addition¶

Addition of two $m \times n$ -dimensional matrices $\textit{A}$ and $\textit{B}$ is defined as a new matrix $\textit{C}$, written $\textit{C} = \textit{A} + \textit{B}$, whose components $c_{ij}$ are given by addition of each component of the two matrices, $c_{ij} = a_{ij}+b_{ij}$.

Matrix Equality¶

Two matrices are equal when they share the same dimensions and all elements are equal. I.e.: $a_{ij}=b_{ij}$ for all $i \in I$ and $j \in J$.

Properties of Matrices¶

For three matrices $\mathbf{A}$, $\mathbf{B}$, and $\mathbf{C}$ we have the following properties

  1. Commutative Law of Addition: $\mathbf{A} + \mathbf{B} = \mathbf{B} + \mathbf{A}$

  2. Associative Law of Addition: $(\mathbf{A} + \mathbf{B}) + \mathbf{C} = \mathbf{A} + (\mathbf{B} + \mathbf{C})$

  3. Associative Law of Multiplication: $\mathbf{A}(\mathbf{B}\mathbf{C}) = (\mathbf{A}\mathbf{B})\mathbf{C}$

  4. Distributive Law: $\mathbf{A}(\mathbf{B} + \mathbf{C}) = \mathbf{A}\mathbf{B} + \mathbf{A}\mathbf{C}$

  5. Identity: There is the matrix equivalent of one. We define a matrix $\mathbf{I_n}$ of dimension $n \times n$ such that the elements of $\mathbf{I_n}$ are all zero, except the diagonal elements $i=j$; where $I_{i,i} = 1$

  6. Zero: We define a matrix $\mathbf 0$ of $m \times n$ dimension as the matrix where all components $(\mathbf 0)_{i,j}$ are 0

Identity Matrix¶

$I_3 = \begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0 \\ 0 & 0 & 1\\ \end{bmatrix}$

Here we can write $\textit{I}\textit{B} = \textit{B}\textit{I} = \textit{B}$ or $\textit{I}\textit{I} = \textit{I}$

Again, it is important to reiterate that matrices are not in general commutative with respect to multiplication. That is to say that the left and right products of matrices are, in general different.

$AB \neq BA$

Matrix Transpose¶

The transpose of a matrix $\textit{A}$ is formed by interchanging the rows and columns of $\textit{A}$. That is

$a_{ij}^T = a_{ji}$

Example 1:¶

$\textit{A} = \begin{bmatrix} 1 & 2 \\ 0 & 1 \\ \end{bmatrix}$

$\textit{A}^{T} = ?$

Matrix Transpose¶

The transpose of a matrix $\textit{A}$ is formed by interchanging the rows and columns of $\textit{A}$. That is

$a_{ij}^T = a_{ji}$

Example 1:¶

$\textit{A} = \begin{bmatrix} 1 & 2 \\ 0 & 1 \\ \end{bmatrix}$

$\textit{A}^{T} = \begin{bmatrix} 1 & 0 \\ 2 & 1 \\ \end{bmatrix}$

Matrix Transpose¶

The transpose of a matrix $\textit{A}$ is formed by interchanging the rows and columns of $\textit{A}$. That is

$a_{ij}^T = a_{ji}$

Example 2:¶

$\textit{B} = \begin{bmatrix} 1 & 2 \\ 0 & -3 \\ 3 & 1 \\ \end{bmatrix}$

$\textit{B}^{T} = ?$

Matrix Transpose¶

The transpose of a matrix $\mathbf A$ is formed by interchanging the rows and columns of $\mathbf A$. That is

$(\mathbf A)^T_{ij} = A_{ji}$

Example 2:¶

$\mathbf B = \begin{bmatrix} 1 & 2 \\ 0 & -3 \\ 3 & 1 \\ \end{bmatrix}$

$\mathbf{B}^{T} = \begin{bmatrix} 1 & 0 & 3 \\ 2 & -3 & 1 \\ \end{bmatrix}$

BONUS:¶

Show that $(\mathbf{A}\mathbf{B})^{T} = \mathbf{B}^{T}\mathbf{A}^{T}$.

Hint: the $ij$th element on both sides is $\sum_{k}A_{jk}A_{ki}$

Matrix-Vector Multiplication¶

Two perspectives:

  1. Linear combination of columns

  2. Dot product of vector with rows of matrix

$\begin{bmatrix} 2 & -6 \\ -1 & 4\\ \end{bmatrix} \begin{bmatrix} 2 \\ -1 \\ \end{bmatrix} = ?$

Test both ways out.

Lab: Matrix-vector multiplication¶

We just defined two different procedures for computing the matrix-vector product. Let us write them in Python.

Suppose we defined vectors as lists, and a matrix as a list of vectors.

  1. Write code to compute the matrix vector product assuming $\mathbf A$ is a list of rows
  2. Write code to compute the matrix vector product assuming $\mathbf A$ is a list of columns

Matrix Multiplication¶

Multiplication of an $m \times n$ -dimensional matrices $\textit{A}$ and a $n \times k$ matrix $\textit{B}$ is defined as a new matrix $\textit{C}$, written $\textit{C} = \textit{A}\textit{B}$, whose elements $C_{ij}$ are

$$ C_{i,j} = \sum_{l=1}^n A_{i,l}B_{l,j} $$

This can be memorized as row by column multiplication, where the value of each cell in the result is achieved by multiplying each element in a given row $i$ of the left matrix with its corresponding element in the column $j$ of the right matrix and adding the result of each operation together. This sum is the value of the new the new component $c_{ij}$.

Note that the product of matrices and vectors is a special case, under the assumption that the vector is oriented correctly and is of correct dimension (same rules as a matrix). In this case, we simply treat the vector as a $n \times 1$ or $1 \times n$ matrix.

Also note that $\textit{B}\textit{A} \neq \textit{A}\textit{B}$ in general.

Example 1:¶

$\textit{C} = \textit{A}\textit{B} = \begin{bmatrix} 1 & 2 \\ 0 & 1 \\ \end{bmatrix} \begin{bmatrix} 2 & 0 \\ 1 & 4 \\ \end{bmatrix} = \begin{bmatrix} 4 & 8 \\ 1 & 4 \\ \end{bmatrix}$

Example 2:¶

$\begin{bmatrix} 1 & 2 \\ 0 & -3 \\ 3 & 1 \\ \end{bmatrix} \begin{bmatrix} 2 & 6 & -3 \\ 1 & 4 & 0 \\ \end{bmatrix} = ?$

Example 2:¶

$\begin{bmatrix} 1 & 2 \\ 0 & -3 \\ 3 & 1 \\ \end{bmatrix} \begin{bmatrix} 2 & 6 & -3 \\ 1 & 4 & 0 \\ \end{bmatrix} = \begin{bmatrix} 4 & 14 & -3\\ -3 & -12 & 0 \\ 7 & 22 & -9\\ \end{bmatrix}$

Example 3:¶

$\begin{bmatrix} 2 & 6 & -3 \\ 1 & 4 & 0 \\ \end{bmatrix} \begin{bmatrix} 1 & 2 \\ 0 & -3 \\ 3 & 1 \\ \end{bmatrix} = ?$

Example 3:¶

$\begin{bmatrix} 2 & 6 & -3 \\ 1 & 4 & 0 \\ \end{bmatrix} \begin{bmatrix} 1 & 2 \\ 0 & -3 \\ 3 & 1 \\ \end{bmatrix} = \begin{bmatrix} -7 & -17\\ 1 & -10 \\ \end{bmatrix}$

Example 4:¶

$\begin{bmatrix} 2 & -6 \\ -1 & 4\\ \end{bmatrix} \begin{bmatrix} 1 \\ 0 \\ \end{bmatrix} = ?$

Example 4:¶

$\begin{bmatrix} 2 & -6 \\ -1 & 4\\ \end{bmatrix} \begin{bmatrix} 1 \\ 0 \\ \end{bmatrix} = \begin{bmatrix} 2\\ -1\\ \end{bmatrix}$

QUIZ:¶

Can you take the product of $\begin{bmatrix} 2 & -6 \\ -1 & 4\\ \end{bmatrix}$ and $\begin{bmatrix} 12 & 46 \\ \end{bmatrix}$ ?

If question seems vague, list all possible ways to address this question.

Lab: Matrix-matrix multiplication¶

There are yet more ways to programmatically implement matrix multiplication

Let us focus on just the two which are direct extensions of the preview matrix-vector multiplication methods

Use your dense vector functions to perform vector matrix multiplication - both by columns and by rows