BDS 761: Data Science and Machine Learning I

Topic 6: Norms, Distances, & Statistics
This topic:¶
- Norms & Distances with Python
- Simple distance-based classification
- Clustering
- Statistics with Python
Reading:
- I2ALA Chapter 3 (Norms), Chapter 4 (Clustering)
- “Linear Algebra and Learning from Data”, Gilbert Strang, Wellesley-Cambridge Press 2019, I.11 (I.11 Norms of Vectors, Functions, and Matrices)
Metric¶
Basically, boil multiple numbers (vectors, matrices, time series,...) or entire functions down to a single number
Examples
- GDP of economy
- BMI (body-mass index)
- A statistic (mean, variance, ...)
- Vector norms...
Always can be critized as discarding important info, but need to use something
Euclidean Norm¶
$$ \|x\| = \sqrt{x_1^2+x_2^2+\dotsb+x_n^2} $$
"Length" of a vector (as opposed to length of the data structure, i.e. number of dimensions)
Also known as $\|x\|_2$, the "two-norm"
Example¶
$$\left\Vert \begin{pmatrix}2 \\ -1\\2 \end{pmatrix}\right\Vert = ?$$
Also use a built-in function to do this
Exercise: give Euclidean norm using dot products
Root-mean-square value (RMS)¶
$$ rms(x) = \sqrt{\frac{x_1^2+x_2^2+\dotsb+x_n^2}{n}} = \frac{1}{\sqrt{n}}\|x\| $$
root(mean(square(x)))
Exercise: give Euclidean norm of sum of vectors $x+y$ in terms of dot products
(use result of previous exercise and work only with vectors)
$$||x+y||_2 = \text{dot}(?,?) + \text{dot}(?,?) + ???$$
$$ \sqrt{(x_1+y_1)*(x_1+y_1) + (x_2+y_2)*(x_2+y_2) + ... } = $$
Chebychev Inequality¶
If $x$ is a length-$n$ vector with $k$ entries satisfying $|x_i|\ge a$ for some constant $a>0$, then
$$\frac{k}{n} \le \left( \frac{rms(x)}{a}\right)^2$$
Basically tells how much elements can deviate from the rms
Derive by noting that $\Vert x\Vert^2 \ge ka^2$
Motivation for other types of norms¶
Consider the list of data for different "dimensions", for one person, product, etc.
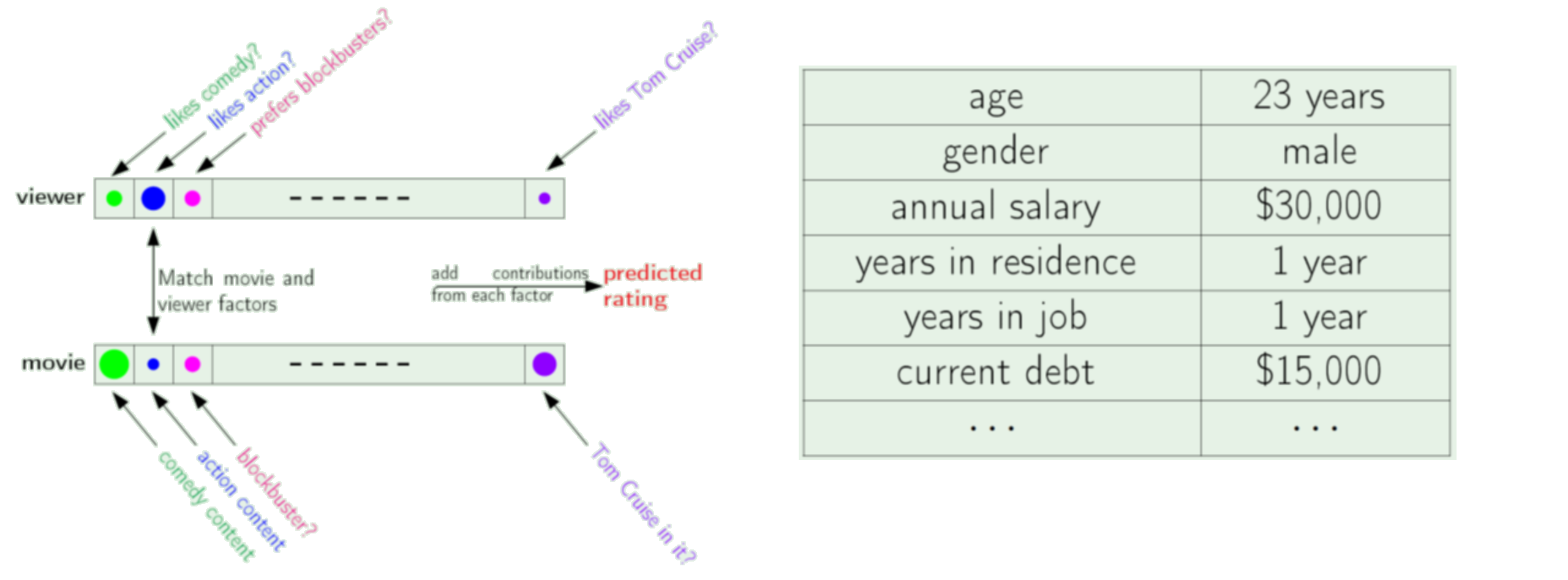
Does it make sense to compute Euclidean distance to tell us how "big" the vector is?
Norms¶
A norm is a vector "length". Often denoted generally as $\Vert \mathbf x \Vert$.
Properties
- Non-negativity: $\Vert \mathbf x \Vert \geq 0$
- Zero upon equality: $\Vert \mathbf x \Vert = 0 \iff \mathbf x = \mathbf 0$
- Absolute scalability: $\Vert \alpha \mathbf x \Vert = |\alpha| \Vert \mathbf x \Vert$ for scalar $\alpha$
- Triangle Inequality: $\Vert \mathbf x + \mathbf z\Vert \leq \Vert \mathbf x\Vert + \Vert \mathbf z\Vert$
$p$-Norms¶
For any $n$-dimensional real or complex vector. i.e. $x \in \mathbb{R}^n \text{ or } \mathbb{C}^n$
$$ \|x\|_p = \left(|x_1|^p+|x_2|^p+\dotsb+|x_n|^p\right)^{\frac{1}{p}} $$
$$ \|x\|_p = \begin{pmatrix}\sum_{i=1}^n{|x_i|^p} \end{pmatrix}^{\frac{1}{p}} $$
Consider the norms we have looked at. What is $p$?
Famous "norms"¶
- $\ell_2$ norm
- $\ell_1$ norm
- $\ell_\infty$ norm
- $\ell_p$ norm
- "$\ell_0$" norm
Note we often lazily write these as e.g. "L2" norm
Exercise: Wite out the $p$-norms for a vector $x$ for $p$ = 1,2,0,$\infty$... $ \|x\|_p = \begin{pmatrix}\sum_{i=1}^n{|x_i|^p} \end{pmatrix}^{\frac{1}{p}} $
Exercise: test the conditions for each
import numpy as np
v = [1,3,1,4]
for p in range(1,10):
print(p,np.power(sum(np.power(np.abs(np.array(v)),p)),1/p))
1 9.0 2 5.196152422706632 3 4.530654896083492 4 4.290915128445443 5 4.175344598847825 6 4.110988070009078 7 4.0723049678331895 8 4.048006070825583 9 4.032310478684122
Exercise¶
What are the norms of $\vec{a} = \begin{bmatrix}1\\3\\1\\-4\end{bmatrix}$ and $\vec{b} = \begin{bmatrix}2\\0\\1\\-2\end{bmatrix}$?
"Norm balls"¶
The Set $\{x | \Vert x \Vert_p \le 1 \}$, $ \|x\|_p = \begin{pmatrix}\sum_{i=1}^n{|x_i|^p} \end{pmatrix}^{\frac{1}{p}} $
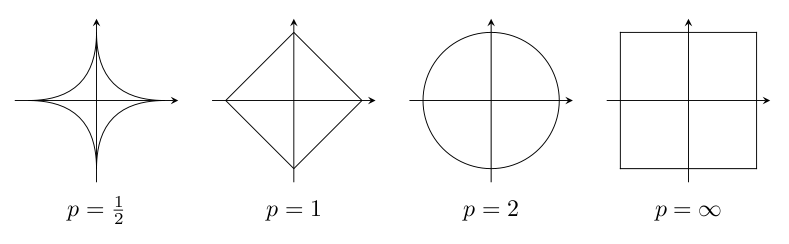
Note how $\Vert x \Vert_a \le \Vert x \Vert_b$ if $a\ge b$
Norms, Inner products, and angles¶
Inner product = length squared
$$v \cdot v = v^T v = \| v \|_2$$
Angle $\theta$ between two vectors
$$v \cdot w = v^T w = \| v \|_2\| w \|_2 \cos\theta$$
Cauchy-Schwartz Inequality $v^T w \le \| v \|\| w \|$¶
Triangle Inequality¶
$$\| v + w \| \le \| v \|+\| w \|$$
Derive by noting that $\| v + w \|^2 = \|v\|^2 + v^Tw + \|w\|^2$ then use Cauchy-Schwartz and complete square
$S$ inner product¶
$$<v,w>_S = v^T S w$$
Minkowski metric¶
Proposed by Lorentz for 4-dimensional spacetime, $v = (x,y,z,t)^T$, $c$ is speed of light
$$\| v\|^2_M = x^2+y^2+z^2-ct^2$$
Is it a true norm?
II. Distances¶
Euclidean distance between two vectors $a$ and $b$ in $\mathbb{R}^{n}$:¶
$$d(\mathbf a,\mathbf b) = \sqrt{\sum_{i=1}^{n}(b_i-a_i)^2}$$
Again this may not make sense for various vectors. Many alternatives...
Norm versus Distance¶
What is the relationship?
Distance properties¶
A distance metic $d(\mathbf x,\mathbf y)$ must satisfy four particular conditions to be considered a metric:
- Non-negativity: $d(\mathbf x,\mathbf y) \geq 0$
- Zero upon equality: $d(\mathbf x,\mathbf y) = 0 \iff \mathbf x = \mathbf y$
- Commutativity of arguments: $d(\mathbf x,\mathbf y) = d(\mathbf y,\mathbf x)$
- Triangle Inequality: $d(\mathbf x,\mathbf z) \leq d(\mathbf x,\mathbf y) + d(\mathbf y,\mathbf z)$
Exercise¶
Write the Euclidean distance between two points entirely in terms of dot products.
What does this tell you about using dot products to compare vector similarity?
Triangle Inequality¶
$\Vert \mathbf x + \mathbf z\Vert \leq \Vert \mathbf x\Vert + \Vert \mathbf z\Vert$
$d(\mathbf a,\mathbf c) \leq d(\mathbf a,\mathbf b) + d(\mathbf b,\mathbf c)$
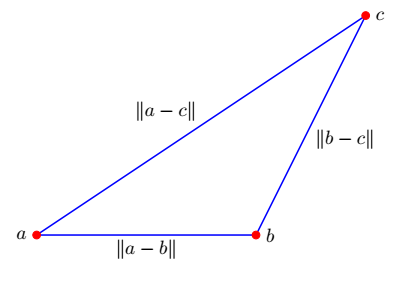
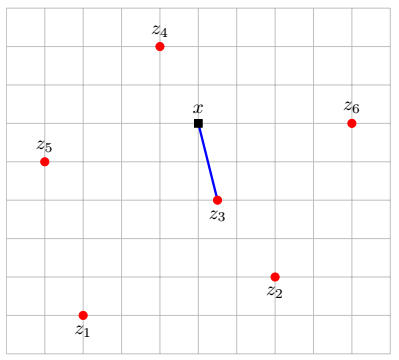
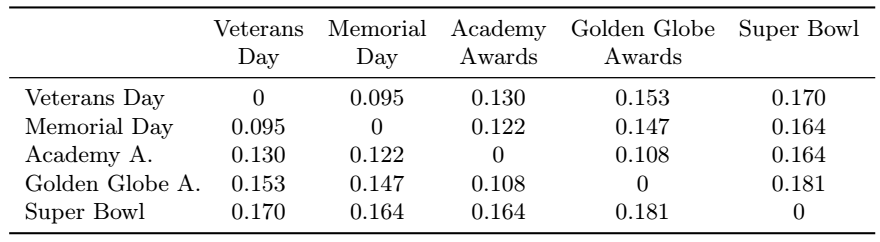
Application: feature distances¶
Recommender syatem based on most similar customers to movie properties

Question: what are the units of the distance here?
Application: rms prediction error¶
Time series prediction (stocks or temperature) compared to truth in retrospect
Manhattan or "Taxicab" Distance, also "Rectilinear distance"¶
Measures the relationships between points at right angles, meaning that we sum the absolute value of the difference in vector coordinates.
This metric is sensitive to rotation.
$$d_{M}(a,b) = \sum_{i=1}^{n}|b_i-a_i|$$
...consider
- Non-negativity: $d(\mathbf x,\mathbf y) \geq 0$
- Zero upon equality: $d(\mathbf x,\mathbf y) = 0 \iff \mathbf x = \mathbf y$
- Commutativity of arguments: $d(\mathbf x,\mathbf y) = d(\mathbf y,\mathbf x)$
- Triangle Inequality: $d(\mathbf x,\mathbf z) \leq d(\mathbf x,\mathbf y) + d(\mathbf y,\mathbf z)$
Exercise¶
Does it fulfill the 4 conditions?
Chebyschev Distance¶
The Chebyschev distance or sometimes the $L^{\infty}$ metric, between two vectors is simply the the greatest of their differences along any coordinate dimension:
$$d_{\infty}(\mathbf a,\mathbf b) = \max_{i}{|(b_i-a_i)|}$$
...consider
- Non-negativity: $d(\mathbf x,\mathbf y) \geq 0$
- Zero upon equality: $d(\mathbf x,\mathbf y) = 0 \iff \mathbf x = \mathbf y$
- Commutativity of arguments: $d(\mathbf x,\mathbf y) = d(\mathbf y,\mathbf x)$
- Triangle Inequality: $d(\mathbf x,\mathbf z) \leq d(\mathbf x,\mathbf y) + d(\mathbf y,\mathbf z)$
Cosine Distance¶
High school geometry: $\mathbf a \cdot \mathbf b = \|\mathbf a\|_2\|\mathbf b\|_2 \cos\theta$
Only depends on angle between the vectors
$$d_{\cos}(\mathbf a,\mathbf b) = 1-\frac{\mathbf a \cdot \mathbf b}{\|\mathbf a\|\|\mathbf b\|} = 1 - \cos\theta$$
Not a true distance metric. which propery fails to hold? (easy to guess at based on geometry)
Exercise¶
Implement the metrics manually and compute distances between:
$ \begin{bmatrix} 1 \\ 2 \\ 3 \\ 4 \end{bmatrix}$ and $ \begin{bmatrix} 5 \\ 6 \\ 7 \\ 8 \end{bmatrix}$
III. Matrix Norms¶
Matrix norms: motivation¶
Same goal as with vector norms: determining if matrices are small or large, or if two matrices are similar or different
Numerical mathematics example: you use 32-bit precision numbers to compute the inverse of a matrix. How different from the true inverse is your numerical calculation? Suppose you used 64-bit precision instead? (FYI the errors can be much larger than $2^{-32}$ or $2^{-64}$)
# https://www.mathworks.com/help/matlab/ref/cond.html
A1 = [[4.1, 2.8],
[9.7, 6.6]]
print(np.linalg.inv(A1))
A2 = [[4.1, 2.8 ],
[9.671, 6.608]]
print(np.linalg.inv(A2))
[[-66. 28.] [ 97. -41.]] [[ 472. -200. ] [-690.78571429 292.85714286]]
Matrix norms¶
The set of matrices can be viewed as a vector space (contains origin, closed under addition and scalar multiplication), hence we can define a norm analogously for lengths and distances
Conditions of a norm
- $\|A\| \ge 0$, only equal if $A$ is zero matrix
- $\|cA\| = |c| \|A\|$
- $\|AB\| \le \|A\|\|B\|$ ...new rule for matrix norms
Matrix norms: Froenius Norm¶
- Frobenius Norm $\Vert A \Vert_F = \sqrt{\sigma_1^2+..+\sigma_r^2} = \sqrt{\sum_{ij}A_{ij}^2}$
Exercise: Compute $\|AB\|_F$
Orthogonal matrix¶
Doesn't change L2 norm of vector or Frobenius norm matrix
$$\Vert Qx\Vert_2 = \Vert x\Vert_2$$
$$\Vert QB\Vert_F = \Vert B\Vert_F$$
Matrix norms from vector norms via vectorization¶
Just "vectorize" the matrix then apply a vector norm.
What do you get if you use the L2 vector norm for this?
Matrix norms from vector norms via matrix-vector product¶
Given a vector norm $\|v\|_\psi$, we can always make a matrix norm as follows
\begin{align} \|A\|_\psi &= \max_{x \ne 0}\dfrac{\Vert Ax \Vert_\psi}{\Vert x\Vert_\psi} \\ &= \max_{x \ne 0, \Vert x\Vert_\psi = 1}\Vert Ax \Vert_\psi \end{align}
What does that give?¶
- $\ell_2$ $\rightarrow$ $\|A\|_2 = \sigma_1$, largest singular value of $A$
- $\ell_1$ $\rightarrow$ $\|A\|_1 = \max_{column_i}\|column_i\|_1 $, largest absolute column sum
- $\ell_\infty$ $\rightarrow$ $\|A\|_\infty = \max_{row_i}\|row_i\|_1 $, largest absolute row sum
Spectral and related norms¶
- Spectral Norm $\Vert A \Vert_2 = \max \dfrac{\Vert Ax \Vert}{\Vert x\Vert} = \sigma_1$, a.k.a. $\ell_2$ norm
- Frobenius Norm $\Vert A \Vert_F = \sqrt{\sigma_1^2+..+\sigma_r^2} = \sqrt{\sum_{ij}A_{ij}^2}$
- Nuclear norm $\Vert A \Vert_N = \sigma_1+..+\sigma_r$, a.k.a. trace norm
Exercise: compute norms for $I$
Spectral Radius¶
$$|\lambda|_{\max} = \max_i |\lambda_i|$$
Useful metric that does not fulfill properties of norm
For every posible (true) norm, we have $\|A\| \ge |\lambda|_{\max}$
Useful fact: if $|\lambda|_{\max} <1$, $\|A^k\| \rightarrow 0$ for large $k$
Can you explain why this happens?
"Medical norm"¶
$$|||A|||_\infty = \max_{i,j}|A_{i,j}|$$
Not a true matrix norm unless scaled properly also
See Strang problem I.11 #12.
Condition number¶
Quantifies how much output changes relative to a change in input.
Low condition number - good - "well conditioned"
- a small chance in inputs due to noise or numerical precision only causes a small change in output
Huge condition number - bad - "ill conditioned"
- even a tiny change in inputs can cause a drastic change in outputs. result unreliable
Condition number for solving linear system $Ax=b$¶
- View the function as $x = A^{-1}b$ where input = $b$ and output = $x$.
- Relative fractional error
$$ RFE = \dfrac{\left(\dfrac{\|A^{-1}(b+\delta) - A^{-1}b\|}{\|A^{-1}b\|}\right)} {\left(\dfrac{\|(b+\delta) - b\|}{\|b\|}\right)} = \dfrac{\left(\dfrac{\|A^{-1}\delta\|}{\|A^{-1}b\|}\right)} {\left(\dfrac{\|\delta\|}{\|b\|}\right)} = \dfrac{\|A^{-1}\delta\|}{\|A^{-1}b\|}\dfrac{\|b\|}{\|\delta\|} $$
Taking the max over $b$ and $\delta$ gives
\begin{align} C &= \max_{b,\delta} \dfrac{\|A^{-1}\delta\|}{\|A^{-1}b\|}\dfrac{\|b\|}{\|\delta\|} \\ &= \left(\max_{\delta}\dfrac{\|A^{-1}\delta\|}{\|\delta\|}\right) \left(\max_{b}\dfrac{\|b\|}{\|A^{-1}b\|} \right) \\ &= \|A^{-1}\|\|A\| \end{align}
First term is just definition of matrix norm. For second term, plug in $b = Ax$ and get norm definition also, noting that max will be the same optimizing over $x$ or over $Ax$ since $A$ is full-rank.
"Matrix Condition number"¶
Usually means condition number with L2 norm
Recall $\|A\|_2 = \sigma_\max(A)$
$$C \equiv \|A^{-1}\|_2\|A\|_2 = \dfrac{\sigma_\max(A)}{\sigma_\min(A)}$$
Suppose a matrix is singular? (what does this mean?)
- what are its singular values?
- what is its condition number?
# https://www.mathworks.com/help/matlab/ref/cond.html
A1 = [[4.1, 2.8],
[9.7, 6.6]]
print(np.linalg.inv(A1))
A2 = [[4.1, 2.8 ],
[9.671, 6.608]]
print(np.linalg.inv(A2))
[[-66. 28.] [ 97. -41.]] [[ 472. -200. ] [-690.78571429 292.85714286]]
print(np.linalg.cond(A1),np.linalg.cond(A2))
1622.9993838565106 11560.27884206701
v1 = np.array([1.,2.])
A = np.array([v1,2.*v1])
print(A)
print('rank =',np.linalg.matrix_rank(A))
[[1. 2.] [2. 4.]] rank = 1
An = A + 1e-10*np.random.rand(2,2)
print('rank =',np.linalg.matrix_rank(An))
print('cond =',np.linalg.cond(An))
rank = 2 cond = 282960980020.97266
Exercise¶
Test the prior matrices when solving a linear system $Ax=b$ and adding a small perturbation to $b$
Change the matrix to make it wekk conditioned and repeat,
IV. Distance-based Classification¶
Lab: simple classification with distances¶
Load and investigate the IRIS dataset from scikit.
Imagine we flower measurements for one of the flowers but don't know the flower type. We want to classify its type by finding the flower of known type which is most similar.
Do this by taking each flower and computing a distance metric between its measurements and that of every other flower. Take the type of the "nearest" flower as your estimate of the flower type.
Compute the accuracy of this technique based on how many flowers are classified correctly in this way.
Try using different distance metrics to compare flowers. Which makes most sense?
from sklearn import datasets
iris = datasets.load_iris()
dir(iris)
['DESCR', 'data', 'feature_names', 'filename', 'target', 'target_names']
(iris.data, iris.target)
(array([[5.1, 3.5, 1.4, 0.2],
[4.9, 3. , 1.4, 0.2],
[4.7, 3.2, 1.3, 0.2],
[4.6, 3.1, 1.5, 0.2],
[5. , 3.6, 1.4, 0.2],
[5.4, 3.9, 1.7, 0.4],
[4.6, 3.4, 1.4, 0.3],
[5. , 3.4, 1.5, 0.2],
[4.4, 2.9, 1.4, 0.2],
[4.9, 3.1, 1.5, 0.1],
[5.4, 3.7, 1.5, 0.2],
[4.8, 3.4, 1.6, 0.2],
[4.8, 3. , 1.4, 0.1],
[4.3, 3. , 1.1, 0.1],
[5.8, 4. , 1.2, 0.2],
[5.7, 4.4, 1.5, 0.4],
[5.4, 3.9, 1.3, 0.4],
[5.1, 3.5, 1.4, 0.3],
[5.7, 3.8, 1.7, 0.3],
[5.1, 3.8, 1.5, 0.3],
[5.4, 3.4, 1.7, 0.2],
[5.1, 3.7, 1.5, 0.4],
[4.6, 3.6, 1. , 0.2],
[5.1, 3.3, 1.7, 0.5],
[4.8, 3.4, 1.9, 0.2],
[5. , 3. , 1.6, 0.2],
[5. , 3.4, 1.6, 0.4],
[5.2, 3.5, 1.5, 0.2],
[5.2, 3.4, 1.4, 0.2],
[4.7, 3.2, 1.6, 0.2],
[4.8, 3.1, 1.6, 0.2],
[5.4, 3.4, 1.5, 0.4],
[5.2, 4.1, 1.5, 0.1],
[5.5, 4.2, 1.4, 0.2],
[4.9, 3.1, 1.5, 0.2],
[5. , 3.2, 1.2, 0.2],
[5.5, 3.5, 1.3, 0.2],
[4.9, 3.6, 1.4, 0.1],
[4.4, 3. , 1.3, 0.2],
[5.1, 3.4, 1.5, 0.2],
[5. , 3.5, 1.3, 0.3],
[4.5, 2.3, 1.3, 0.3],
[4.4, 3.2, 1.3, 0.2],
[5. , 3.5, 1.6, 0.6],
[5.1, 3.8, 1.9, 0.4],
[4.8, 3. , 1.4, 0.3],
[5.1, 3.8, 1.6, 0.2],
[4.6, 3.2, 1.4, 0.2],
[5.3, 3.7, 1.5, 0.2],
[5. , 3.3, 1.4, 0.2],
[7. , 3.2, 4.7, 1.4],
[6.4, 3.2, 4.5, 1.5],
[6.9, 3.1, 4.9, 1.5],
[5.5, 2.3, 4. , 1.3],
[6.5, 2.8, 4.6, 1.5],
[5.7, 2.8, 4.5, 1.3],
[6.3, 3.3, 4.7, 1.6],
[4.9, 2.4, 3.3, 1. ],
[6.6, 2.9, 4.6, 1.3],
[5.2, 2.7, 3.9, 1.4],
[5. , 2. , 3.5, 1. ],
[5.9, 3. , 4.2, 1.5],
[6. , 2.2, 4. , 1. ],
[6.1, 2.9, 4.7, 1.4],
[5.6, 2.9, 3.6, 1.3],
[6.7, 3.1, 4.4, 1.4],
[5.6, 3. , 4.5, 1.5],
[5.8, 2.7, 4.1, 1. ],
[6.2, 2.2, 4.5, 1.5],
[5.6, 2.5, 3.9, 1.1],
[5.9, 3.2, 4.8, 1.8],
[6.1, 2.8, 4. , 1.3],
[6.3, 2.5, 4.9, 1.5],
[6.1, 2.8, 4.7, 1.2],
[6.4, 2.9, 4.3, 1.3],
[6.6, 3. , 4.4, 1.4],
[6.8, 2.8, 4.8, 1.4],
[6.7, 3. , 5. , 1.7],
[6. , 2.9, 4.5, 1.5],
[5.7, 2.6, 3.5, 1. ],
[5.5, 2.4, 3.8, 1.1],
[5.5, 2.4, 3.7, 1. ],
[5.8, 2.7, 3.9, 1.2],
[6. , 2.7, 5.1, 1.6],
[5.4, 3. , 4.5, 1.5],
[6. , 3.4, 4.5, 1.6],
[6.7, 3.1, 4.7, 1.5],
[6.3, 2.3, 4.4, 1.3],
[5.6, 3. , 4.1, 1.3],
[5.5, 2.5, 4. , 1.3],
[5.5, 2.6, 4.4, 1.2],
[6.1, 3. , 4.6, 1.4],
[5.8, 2.6, 4. , 1.2],
[5. , 2.3, 3.3, 1. ],
[5.6, 2.7, 4.2, 1.3],
[5.7, 3. , 4.2, 1.2],
[5.7, 2.9, 4.2, 1.3],
[6.2, 2.9, 4.3, 1.3],
[5.1, 2.5, 3. , 1.1],
[5.7, 2.8, 4.1, 1.3],
[6.3, 3.3, 6. , 2.5],
[5.8, 2.7, 5.1, 1.9],
[7.1, 3. , 5.9, 2.1],
[6.3, 2.9, 5.6, 1.8],
[6.5, 3. , 5.8, 2.2],
[7.6, 3. , 6.6, 2.1],
[4.9, 2.5, 4.5, 1.7],
[7.3, 2.9, 6.3, 1.8],
[6.7, 2.5, 5.8, 1.8],
[7.2, 3.6, 6.1, 2.5],
[6.5, 3.2, 5.1, 2. ],
[6.4, 2.7, 5.3, 1.9],
[6.8, 3. , 5.5, 2.1],
[5.7, 2.5, 5. , 2. ],
[5.8, 2.8, 5.1, 2.4],
[6.4, 3.2, 5.3, 2.3],
[6.5, 3. , 5.5, 1.8],
[7.7, 3.8, 6.7, 2.2],
[7.7, 2.6, 6.9, 2.3],
[6. , 2.2, 5. , 1.5],
[6.9, 3.2, 5.7, 2.3],
[5.6, 2.8, 4.9, 2. ],
[7.7, 2.8, 6.7, 2. ],
[6.3, 2.7, 4.9, 1.8],
[6.7, 3.3, 5.7, 2.1],
[7.2, 3.2, 6. , 1.8],
[6.2, 2.8, 4.8, 1.8],
[6.1, 3. , 4.9, 1.8],
[6.4, 2.8, 5.6, 2.1],
[7.2, 3. , 5.8, 1.6],
[7.4, 2.8, 6.1, 1.9],
[7.9, 3.8, 6.4, 2. ],
[6.4, 2.8, 5.6, 2.2],
[6.3, 2.8, 5.1, 1.5],
[6.1, 2.6, 5.6, 1.4],
[7.7, 3. , 6.1, 2.3],
[6.3, 3.4, 5.6, 2.4],
[6.4, 3.1, 5.5, 1.8],
[6. , 3. , 4.8, 1.8],
[6.9, 3.1, 5.4, 2.1],
[6.7, 3.1, 5.6, 2.4],
[6.9, 3.1, 5.1, 2.3],
[5.8, 2.7, 5.1, 1.9],
[6.8, 3.2, 5.9, 2.3],
[6.7, 3.3, 5.7, 2.5],
[6.7, 3. , 5.2, 2.3],
[6.3, 2.5, 5. , 1.9],
[6.5, 3. , 5.2, 2. ],
[6.2, 3.4, 5.4, 2.3],
[5.9, 3. , 5.1, 1.8]]),
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2]))
iris.data[52]
array([6.9, 3.1, 4.9, 1.5])
The "1-Nearest-Neighbor" Algorithm¶
Example using two features. Dots represent the measurements for the flowers in the dataset. Color of background is class of nearest neighbor (as if the point was the measurements for an unknown flower we were classifying)
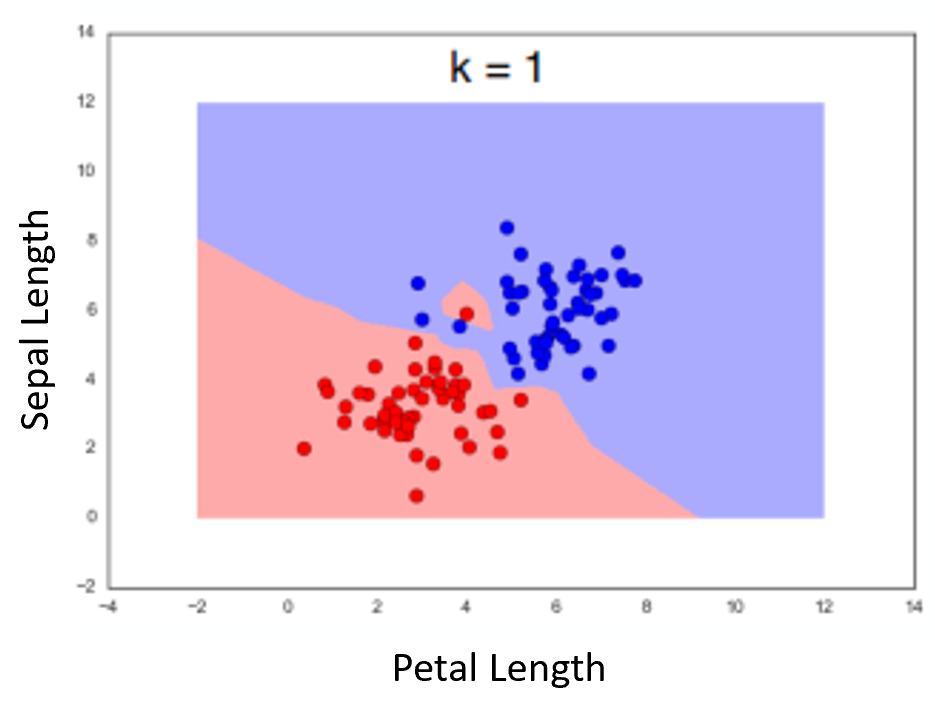
Hamming or "Rook" Distance¶
The hamming distance can be used to compare nearly anything to anything else.
Defined as the number of differences in characters between two strings of equal length, ie:
$$d_{hamming}('bear', 'beat') = 1$$ $$d_{hamming}('cat', 'cog') = 2$$ $$d_{hamming}('01101010', '01011011') = 3$$
Edit distance¶
Similar to hamming distance, but also includes insertions and deletions, and so can compare strings of any length to each other.
$$d_{edit}('lead', 'gold') = 4$$ $$d_{edit}('monkey', 'monk') = 2$$ $$d_{edit}('lucas', 'mallori') = 8$$
- A kind of approximate matching method.
- Must use dynamic programming or memoization for efficiency
V. Clustering¶
Dimensionality Reduction¶
Describing data with less information
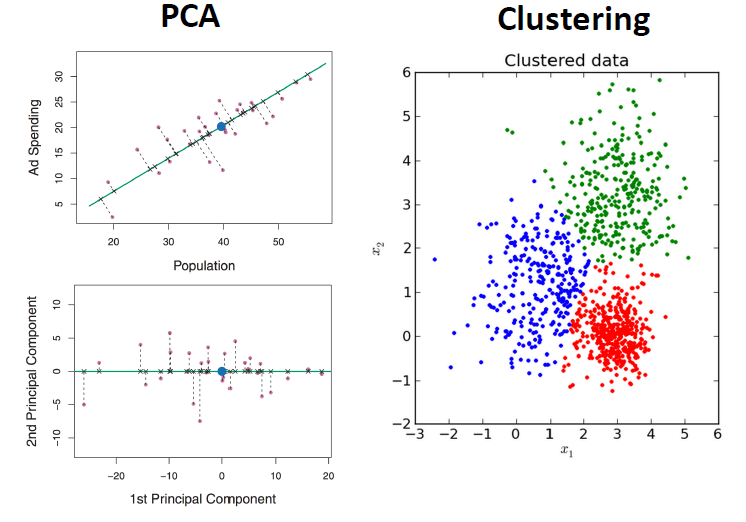
How are PCA and Clustering leading to less information? Consider a dataset.
What are the benefits?
Clustering References¶
https://en.wikipedia.org/wiki/K-means_clustering
https://en.wikipedia.org/wiki/K-means%2B%2B - kmeans++
https://www.youtube.com/watch?v=IuRb3y8qKX4 - video with visualization of training progress
https://www.youtube.com/watch?v=cWSnFaSjgBU - more on visualization
http://scikit-learn.org/stable/modules/generated/sklearn.cluster.KMeans.html
Marketing Motivation¶
You want to make a certain number of products for a large population of customers. We know a number of features describing each of the customers, and are able to target a product to a certain customer profile.
E.g.: different customers prefer cars which are fast, or get good gas mileage, or are cheap, or are luxurious and presigious (i.e., expensive), or are big, or are little, etc. And in various combinations.
The customers vary widely so we wish to make k products which cover as closely as possible what as many as possible customers would like.
The better you can do this, the better your products will sell.
K-means clustering¶
- K clusters, centers are the means of cluster members.
- Each sample belongs to the cluster who's mean is nearest.
- Iteratively recompute membership and means (greedy optimization)
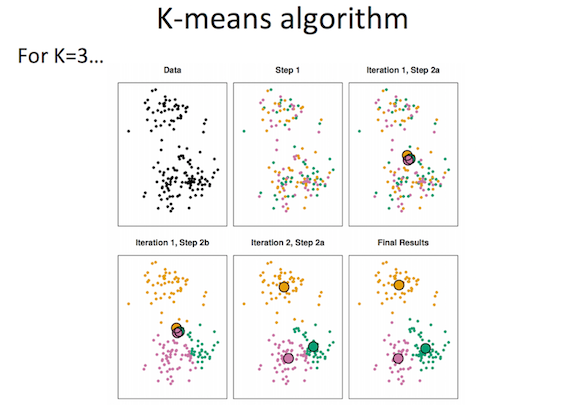
K-means algorithm¶
- Assign a number from 1 to K to each of N data points randomly
- While cluster assignments keep changing:
- For each of K clusters:
- Calculate cluster centroid
- For each of N points:
- Assign point to centroid it is closest to
- For each of K clusters:
Consider the possible ways to vary details in this method? How many clusters? How calculate distance?
k-Means as Greedy Optimization¶
The sum of all distances between members of a cluster gives a total length (a squared length can be viewed as a measure of "energy").
Within-Cluster-Variation: $WCV(C_k) = \dfrac{1}{|C_k|}\sum_{i, j \in C_k}d(x_{i}-x_{j})$, where $d(x_{i}-x_{j})$ is a distance metric of your choice.
k-means tries to minimize the net lengths over all clusters.
If you plotted this for each iteration, what would the plot look like?
Lab¶
Implement k-means clustering algorithm using scikit on IRIS, MNIST datasets.
Compute the net WCV for various options.
Look at result and WCV with different initializations.
Try varying the metric used in the clustering.
Vary k and plot WCV versus k.
Scikit hints¶
Hyperparameter k is input into constructor as usual
Clustering done with a stereotpyical "Fit()" method
Results (cluster centers, cluster label for each point) stuck in attributes, as usual. ".inertia_" ~ WCV)
Variants of k-Means¶
It's often possible by being creative to come up with ways to define a distance for unusual data types.
For example: comparing books with distance defined as (inverse) number of common words. Both contan "the", "soufle", france", etc.
But it still may not make sense to average the data. Why is this a problem? What might be done instead?
Statistics with Python¶
Random sampling¶
- rand() - uniform random numbers in [0,1]
- randn() - standard normal random numbers (zero mean, unit variance)
from numpy import random
printcols(dir(random))
BitGenerator __package__ default_rng noncentral_chisquare set_state Generator __path__ dirichlet noncentral_f shuffle MT19937 __spec__ exponential normal standard_cauchy PCG64 _bounded_integers f pareto standard_exponential PCG64DXSM _common gamma permutation standard_gamma Philox _generator geometric poisson standard_normal RandomState _mt19937 get_state power standard_t SFC64 _pcg64 gumbel rand test SeedSequence _philox hypergeometric randint triangular __RandomState_ctor _pickle laplace randn uniform __all__ _sfc64 logistic random vonmises __builtins__ beta lognormal random_integers wald __cached__ binomial logseries random_sample weibull __doc__ bit_generator mtrand ranf zipf __file__ bytes multinomial rayleigh __loader__ chisquare multivariate_normal sample __name__ choice negative_binomial seed
The Normal Distribution¶
- Also known as Gaussian distribution
$$ f(x) = \frac{1}{\sqrt{2\pi}\sigma} e^{\frac{-(x-\mu)^2}{2\sigma^2}} \text{ for } -\infty < x < \infty $$
\begin{align} E(X) &= \mu \\ V(X) &= \sigma^2 \end{align}
import numpy as np
from matplotlib import pyplot as plt
def univariate_normal(x, mean, var):
return ((1. / np.sqrt(2 * np.pi * var)) * np.exp(-(x - mean)**2 / (2 * var)))
x = np.linspace(-5,5,1000)
plt.plot(x,univariate_normal(x,1,2));
plt.show()
Exercise¶
Generate normal random samples with mean of 1 and variance of 1
Plot histogram versus the theoretical distribution
Try different numbers of samples
Statistics¶
Consider the relation between norms and simple statistical quantities
\begin{align} \text{Population mean} &= \mu = \frac{\sum_{i=1}^N x_i}{N} \\ \text{Sample mean} &= \bar{x} = \frac{\sum_{i=1}^n x_i}{n} \\ \text{Population variance} &= \sigma^2 = \frac{\sum_{i=1}^N (x_i - \mu)^2}{N} \\ \text{Sample variance} &= s^2 = \frac{\sum_{i=1}^n (x_i - \bar{x})^2}{n - 1} = \frac{\sum_{i=1}^n x_i^2 - \frac{1}{n}(\sum_{i=1}^n x_i)^2}{n - 1} \\ \text{Standard deviation} &= \sqrt{\text{Variance}} \end{align}
Exercise¶
Load a dataset from sklearn and compute mean and variance of a column
Standardize the column
Now compute mean and variance of the result
The Standard Normal Distribution $Z$¶
- If $X$ is a normal r.v. with $E(X) = \mu$ and $V(X) = \sigma^2$
$$ Z = \frac{X-\mu}{\sigma} $$
- $Z$ is a normal r.v. with $E(X) = 0$ and $V(X) = 1$
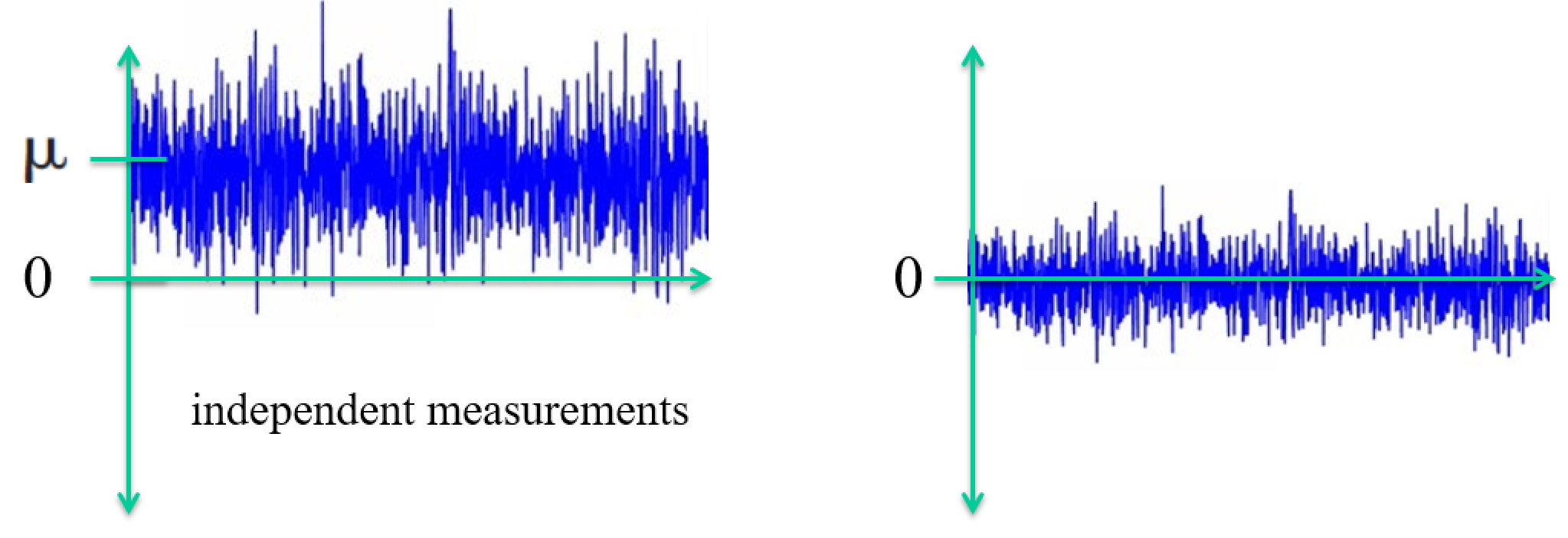
Standardizing data has two tasks¶
$$ Z = \frac{X-\mu}{\sigma} $$
- Remove the mean
- scale by the standard deviation
Lab: Standardizing data¶
Standardize the columns of the Iris dataset using linear algebra.
Test it worked by computing the mean and norm of each column.
Multivariate Gaussian (for $n$ dimensions)¶
$$ f(\mathbf x) = \frac{1}{ \sqrt{2 \pi^n |\boldsymbol\Sigma|}} \exp \left(- \frac{1}{2} (\mathbf x - \boldsymbol \mu)^T \boldsymbol\Sigma^{-1} (\mathbf x - \boldsymbol \mu) \right) \text{, for } \mathbf x \in R^n $$
- Mean vector as centroid of distribution
- Covariance matrix describes spread - correlations between variables $\Sigma_{ij} = S_{\mathbf x_i \mathbf x_j}$
\begin{align} \text{Correlation Coefficient} &= r = \frac{ \sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum_{i=1}^n(x_i - \bar{x})^2}\sqrt{\sum_{i=1}^n(y_i - \bar{y})^2}} = \frac{S_{xy}}{\sqrt{S_{xx} S_{yy}}} \\ %\text{''Corrected Correlation''} % &= S_{xy} = \sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y}) % = \sum_{i=1}^n x_i y_i - \frac{1}{n}(\sum_{i=1}^n x_i)(\sum_{i=1}^n y_i) \\ \text{Covariance} &= S_{xy} = \frac{1}{n-1}\sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y}) % = \sum_{i=1}^n x_i y_i - \frac{1}{n}(\sum_{i=1}^n x_i)(\sum_{i=1}^n y_i) \end{align}
def multivariate_normal(x, n, mean, cov):
return (1./(np.sqrt((2*np.pi)**n * np.linalg.det(cov))) * np.exp(-1/2*(x - mean).T@np.linalg.inv(cov)@(x - mean)))
mean = np.array([35,70])
cov = 100*np.array([[1,.5],[.5,1]])
pic = np.zeros((100,100))
for x1 in np.arange(0,100):
for x2 in np.arange(0,100):
x = [x1,x2]
pic[x1,x2] = multivariate_normal(x, 2, mean, cov)
plt.contour(pic);
Tricky Exercise¶
Consider a $m \times 3$ matrix $\mathbf A$ with columns $\mathbf x, \mathbf y$, and $\mathbf z$ (each a vector of data).
How would you efficiently standardize the three columns to make $\bar{\mathbf A}$.
What are the elements of $\bar{\mathbf A}^T \bar{\mathbf A}$?
Exercise:¶
Assume you have a vector containing samples. Write the following in terms of norms and dot products:
- mean
- variance
- Correlation coefficient
- Covariance
So what does this tell you about comparing things using distances versus dot products versus statistics?